EOS: Introduction to the Equation of state

The equation of states (EOS) can be used to compute the minimum lattice constants for a bulk material. In the following, we demonstrate how the ASE Equation of state function can be used to compute the minimum energy lattice constant and pressure for FCC silver.

First, do a bulk calculation for different lattice constants:

import numpy as np

from ase import Atoms
from ase.calculators.emt import EMT
from ase.eos import EquationOfState
from ase.io import read
from ase.io.trajectory import Trajectory
from ase.units import kJ

a = 4.0  # approximate lattice constant
b = a / 2
ag = Atoms(
    'Ag', cell=[(0, b, b), (b, 0, b), (b, b, 0)], pbc=1, calculator=EMT()
)  # use EMT potential
cell = ag.get_cell()
traj = Trajectory('Ag.traj', 'w')
for x in np.linspace(0.95, 1.05, 5):
    ag.set_cell(cell * x, scale_atoms=True)
    ag.get_potential_energy()
    traj.write(ag)

This writes a trajectory file containing five configurations of FCC silver for five different lattice constants. Now, analyse the result with the EquationOfState class:

configs = read('Ag.traj@0:5')  # read 5 configurations
# Extract volumes and energies:
volumes = [ag.get_volume() for ag in configs]
energies = [ag.get_potential_energy() for ag in configs]
eos = EquationOfState(volumes, energies)
v0, e0, B = eos.fit()
print(B / kJ * 1.0e24, 'GPa')
eos.plot('Ag-eos.png')

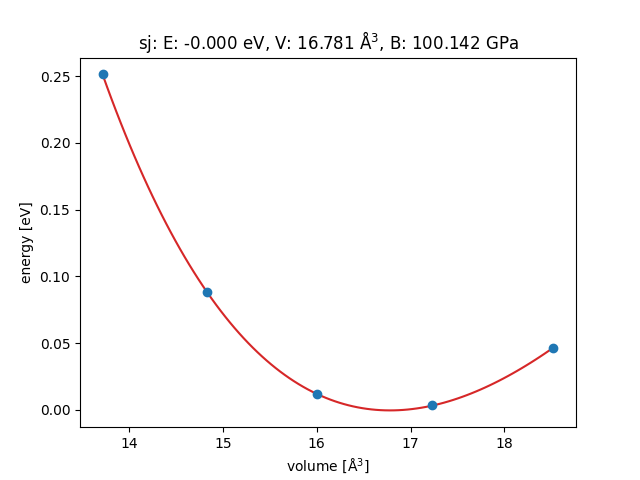
100.14189241973199 GPa

<Axes: title={'center': 'sj: E: -0.000 eV, V: 16.781 Å$^3$, B: 100.142 GPa'}, xlabel='volume [Å$^3$]', ylabel='energy [eV]'>

A quicker way to do this analysis is to use the ase.gui tool:

$   ase gui Ag.traj

And then choose Tools ‣ Bulk modulus.