Note
Go to the end to download the full example code.
NEB with IDPP: Image Dependent Pair Potential for improved interpolation of NEB initial guess#
Reference: S. Smidstrup, A. Pedersen, K. Stokbro and H. Jonsson, Improved initial guess for minimum energy path calculations, J. Chem. Phys. 140, 214106 (2014).
Use of the Nudged Elastic Band (NEB) method for transition state search is dependent upon generating an initial guess for the images lying between the initial and final states. The most simple approach is to use linear interpolation of the atomic coordinates. However, this can be problematic as the quality of the interpolated path can ofter be far from the real one. The implication being that a lot of time is spent in the NEB routine optimising the shape of the path, before the transition state is homed-in upon.
The image dependent pair potential (IDPP) is a method that has been developed to provide an improvement to the initial guess for the NEB path. The IDPP method uses the bond distance between the atoms involved in the transition state to create target structures for the images, rather than interpolating the atomic positions. By defining an objective function in terms of the distances between atoms, the NEB algorithm is used with this image dependent pair potential to create the initial guess for the full NEB calculation.
Note
The examples below utilise the EMT calculator for illustrative purposes, the results should not be over interpreted.
This tutorial includes example NEB calculations for two different systems. First, it starts with a simple NEB of Ethane comparing IDPP to the standard linear approach. The second example is for a N atom on a Pt step edge.
Example 1: Ethane#
This example illustrates the use of the IDPP interpolation scheme to generate an initial guess for rotation of a methyl group around the CC bond.
1.1 Generate Initial and Final State#
Step Time Energy fmax
FIRE: 0 11:11:31 3.078940 4.012422
FIRE: 1 11:11:31 2.530571 3.506100
FIRE: 2 11:11:31 1.950051 2.538108
FIRE: 3 11:11:31 1.752270 1.148539
FIRE: 4 11:11:31 1.732747 1.108297
FIRE: 5 11:11:31 1.696342 1.027750
FIRE: 6 11:11:31 1.648051 0.907203
FIRE: 7 11:11:31 1.594621 0.748189
FIRE: 8 11:11:31 1.543597 0.554845
FIRE: 9 11:11:31 1.502047 0.532019
FIRE: 10 11:11:31 1.475189 0.516589
FIRE: 11 11:11:31 1.465461 0.338747
FIRE: 12 11:11:31 1.465228 0.325538
FIRE: 13 11:11:31 1.464795 0.299554
FIRE: 14 11:11:31 1.464228 0.261663
FIRE: 15 11:11:31 1.463608 0.213166
FIRE: 16 11:11:31 1.463029 0.155784
FIRE: 17 11:11:31 1.462575 0.091667
FIRE: 18 11:11:31 1.462314 0.029444
np.True_
Let’s look at the relaxed molecule.
import matplotlib.pyplot as plt
from ase.visualize.plot import plot_atoms
fig, ax = plt.subplots()
plot_atoms(initial, ax, rotation=('90x,0y,90z'))
ax.set_axis_off()
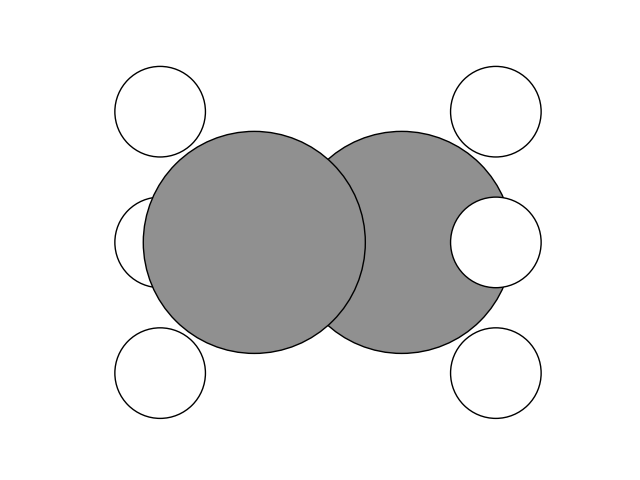
Now we can create the final state. Since we want to look at the rotation of the methyl group, we switch the position of the Hydrogen atoms on one methyl group. Then, we setup and run the NEB calculation.
final = initial.copy()
final.positions[2:5] = initial.positions[[3, 4, 2]]
1.2 Linear Interpolation Approach#
Generate blank images.
images = [initial]
for i in range(9):
images.append(initial.copy())
for image in images:
image.calc = EMT()
images.append(final)
# Run linear interpolation.
neb = NEB(images)
neb.interpolate()
# Run NEB calculation.
qn = FIRE(neb, trajectory='ethane_linear.traj')
qn.run(fmax=0.05)
# You can add a logfile to the FIRE optimizer by adding
# e.g. `logfile='ethane_linear.log` to save the printed output.
Step Time Energy fmax
FIRE: 0 11:11:31 16.807663 53.427700
FIRE: 1 11:11:31 8.983628 30.051463
FIRE: 2 11:11:31 4.994438 15.778800
FIRE: 3 11:11:31 3.174875 8.541174
FIRE: 4 11:11:31 2.414002 6.012149
FIRE: 5 11:11:31 2.361747 8.473474
FIRE: 6 11:11:31 2.489129 10.566475
FIRE: 7 11:11:31 2.149957 8.085552
FIRE: 8 11:11:31 1.759915 4.220557
FIRE: 9 11:11:31 1.617775 1.150575
FIRE: 10 11:11:31 1.630155 2.980283
FIRE: 11 11:11:31 1.618059 2.829342
FIRE: 12 11:11:31 1.596862 2.540181
FIRE: 13 11:11:31 1.569987 2.122334
FIRE: 14 11:11:31 1.541420 1.604189
FIRE: 15 11:11:31 1.516393 1.015755
FIRE: 16 11:11:31 1.501620 0.582353
FIRE: 17 11:11:31 1.490385 0.502925
FIRE: 18 11:11:31 1.482024 0.839500
FIRE: 19 11:11:31 1.480582 1.293310
FIRE: 20 11:11:31 1.483450 1.585808
FIRE: 21 11:11:31 1.483989 1.630022
FIRE: 22 11:11:31 1.477501 1.392580
FIRE: 23 11:11:31 1.466825 0.875317
FIRE: 24 11:11:31 1.460922 0.262243
FIRE: 25 11:11:31 1.460753 0.258842
FIRE: 26 11:11:31 1.460425 0.252318
FIRE: 27 11:11:31 1.459959 0.242638
FIRE: 28 11:11:31 1.459384 0.229928
FIRE: 29 11:11:31 1.458734 0.214364
FIRE: 30 11:11:31 1.458046 0.196170
FIRE: 31 11:11:32 1.457503 0.175489
FIRE: 32 11:11:32 1.457327 0.150641
FIRE: 33 11:11:32 1.457134 0.120917
FIRE: 34 11:11:32 1.456937 0.101103
FIRE: 35 11:11:32 1.456753 0.132701
FIRE: 36 11:11:32 1.456608 0.150041
FIRE: 37 11:11:32 1.456531 0.142591
FIRE: 38 11:11:32 1.456537 0.104226
FIRE: 39 11:11:32 1.456536 0.102178
FIRE: 40 11:11:32 1.456534 0.098128
FIRE: 41 11:11:32 1.456531 0.092173
FIRE: 42 11:11:32 1.456527 0.084463
FIRE: 43 11:11:32 1.456523 0.075201
FIRE: 44 11:11:32 1.456518 0.064646
FIRE: 45 11:11:32 1.456512 0.053119
FIRE: 46 11:11:32 1.456504 0.046413
np.True_
Using the standard linear interpolation approach, as in the following example, we can see that 47 iterations are required to find the transition state.
1.3 Image Dependent Pair Potential#
However if we modify our script slightly and use the IDPP method to find the initial guess, we can see that the number of iterations required to find the transition state is reduced to 7.
# Optimise molecule.
initial = molecule('C2H6')
initial.calc = EMT()
relax = FIRE(initial, logfile='opt.log')
relax.run(fmax=0.05)
# Create final state.
final = initial.copy()
final.positions[2:5] = initial.positions[[3, 4, 2]]
# Generate blank images.
images = [initial]
for i in range(9):
images.append(initial.copy())
for image in images:
image.calc = EMT()
images.append(final)
# Run IDPP interpolation.
neb = NEB(images)
neb.interpolate('idpp')
# Run NEB calculation.
qn = FIRE(neb, trajectory='ethane_idpp.traj')
qn.run(fmax=0.05)
Step Time Energy fmax
FIRE: 0 11:11:32 1.476068 0.897816
FIRE: 1 11:11:32 1.464290 0.433330
FIRE: 2 11:11:32 1.460766 0.265388
FIRE: 3 11:11:32 1.460734 0.235198
FIRE: 4 11:11:32 1.460674 0.178442
FIRE: 5 11:11:32 1.460596 0.102263
FIRE: 6 11:11:32 1.460510 0.044589
np.True_
Clearly, if one was using a full DFT calculator one can potentially gain a significant time improvement.
Example 2: N Diffusion over a Step Edge#
Often we are interested in generating an initial guess for a surface reaction.
2.1 Generate Initial and Final State#
The first part of this example illustrates how we can optimise our initial and final state structures before using the IDPP interpolation to generate our initial guess for the NEB calculation:
import numpy as np
from ase import Atoms
from ase.calculators.emt import EMT
from ase.constraints import FixAtoms
from ase.lattice.cubic import FaceCenteredCubic
from ase.mep import NEB
from ase.optimize.fire import FIRE as FIRE
# Set the number of images you want.
nimages = 5
# Some algebra to determine surface normal and the plane of the surface.
d3 = [2, 1, 1]
a1 = np.array([0, 1, 1])
d1 = np.cross(a1, d3)
a2 = np.array([0, -1, 1])
d2 = np.cross(a2, d3)
# Create the slab.
slab = FaceCenteredCubic(
directions=[d1, d2, d3], size=(2, 1, 2), symbol=('Pt'), latticeconstant=3.9
)
# Add some vacuum to the slab.
uc = slab.get_cell()
uc[2] += [0.0, 0.0, 10.0] # There are ten layers of vacuum.
uc = slab.set_cell(uc, scale_atoms=False)
# Some positions needed to place the atom in the correct place.
x1 = 1.379
x2 = 4.137
x3 = 2.759
y1 = 0.0
y2 = 2.238
z1 = 7.165
z2 = 6.439
# Add the adatom to the list of atoms and set constraints of surface atoms.
slab += Atoms('N', [((x2 + x1) / 2, y1, z1 + 1.5)])
FixAtoms(mask=slab.symbols == 'Pt')
# Optimise the initial state: atom below step.
initial = slab.copy()
initial.calc = EMT()
relax = FIRE(initial, logfile='opt.log')
relax.run(fmax=0.05)
np.True_
Now let’s visualize this.
fig, ax = plt.subplots()
plot_atoms(initial, ax, rotation=('0x,0y,0z'))
ax.set_axis_off()
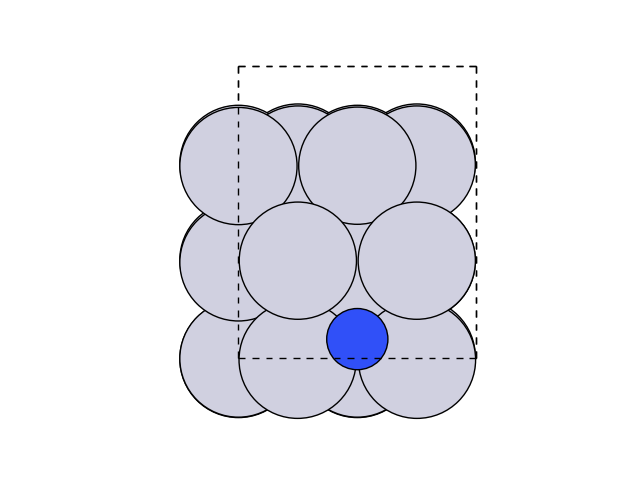
We can now create and optimise the final state by moving the atom above the step.
np.True_
Now let’s visualize this.
fig, ax = plt.subplots()
plot_atoms(final, ax, rotation=('0x,0y,0z'))
ax.set_axis_off()
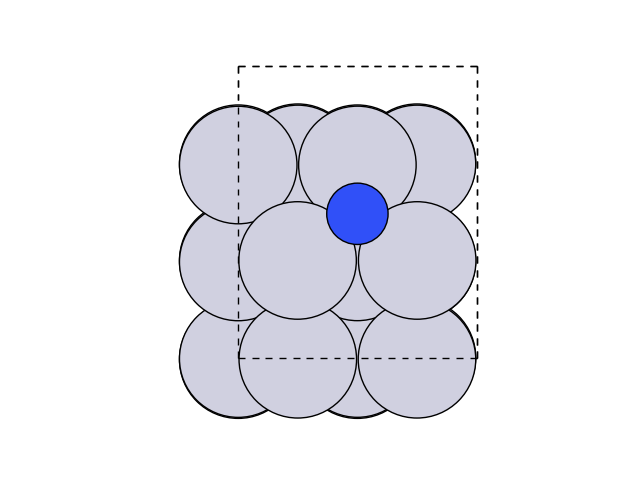
2.2 Image Dependent Pair Potential#
Now we are ready to setup the NEB with the IDPP interpolation.
# Create a list of images for interpolation.
images = [initial]
for i in range(nimages):
images.append(initial.copy())
for image in images:
image.calc = EMT()
images.append(final)
# Carry out idpp interpolation.
neb = NEB(images)
neb.interpolate('idpp')
# Run NEB calculation.
qn = FIRE(neb, trajectory='N_diffusion.traj')
qn.run(fmax=0.05)
Step Time Energy fmax
FIRE: 0 11:11:33 4.893581 5.132169
FIRE: 1 11:11:33 4.593734 3.658559
FIRE: 2 11:11:33 4.295829 1.766259
FIRE: 3 11:11:33 4.118538 2.106191
FIRE: 4 11:11:33 4.034242 1.578724
FIRE: 5 11:11:33 4.020221 1.463086
FIRE: 6 11:11:33 3.996038 1.245614
FIRE: 7 11:11:33 3.968079 0.951118
FIRE: 8 11:11:33 3.943079 0.612734
FIRE: 9 11:11:33 3.926501 0.439465
FIRE: 10 11:11:33 3.916502 0.709684
FIRE: 11 11:11:33 3.911408 0.904931
FIRE: 12 11:11:33 3.904926 0.992393
FIRE: 13 11:11:33 3.893839 0.936674
FIRE: 14 11:11:33 3.880481 0.773424
FIRE: 15 11:11:33 3.869332 0.441845
FIRE: 16 11:11:33 3.861446 0.347778
FIRE: 17 11:11:33 3.857222 0.461723
FIRE: 18 11:11:33 3.855963 0.435831
FIRE: 19 11:11:33 3.854111 0.386369
FIRE: 20 11:11:33 3.852173 0.315649
FIRE: 21 11:11:33 3.850225 0.229478
FIRE: 22 11:11:33 3.848597 0.136225
FIRE: 23 11:11:33 3.847479 0.118939
FIRE: 24 11:11:33 3.846838 0.167220
FIRE: 25 11:11:33 3.846431 0.219306
FIRE: 26 11:11:33 3.846381 0.215929
FIRE: 27 11:11:33 3.846284 0.209250
FIRE: 28 11:11:33 3.846146 0.199417
FIRE: 29 11:11:34 3.845973 0.186654
FIRE: 30 11:11:34 3.845775 0.171260
FIRE: 31 11:11:34 3.845560 0.153607
FIRE: 32 11:11:34 3.845339 0.134141
FIRE: 33 11:11:34 3.845096 0.111139
FIRE: 34 11:11:34 3.844840 0.085747
FIRE: 35 11:11:34 3.844580 0.061683
FIRE: 36 11:11:34 3.844318 0.060244
FIRE: 37 11:11:34 3.844046 0.083896
FIRE: 38 11:11:34 3.843742 0.102731
FIRE: 39 11:11:34 3.843374 0.112933
FIRE: 40 11:11:34 3.842918 0.111429
FIRE: 41 11:11:34 3.842376 0.096025
FIRE: 42 11:11:34 3.841792 0.066377
FIRE: 43 11:11:34 3.841244 0.040019
np.True_
2.3 Linear Interpolation Approach#
To again illustrate the potential speedup, the following script uses the linear interpolation. This takes more iterations to find a transition state, compared to using the IDPP interpolation. We start from the initial and final state we generated above.
# Create a list of images for interpolation.
images = [initial]
for i in range(nimages):
images.append(initial.copy())
for image in images:
image.calc = EMT()
images.append(final)
# Carry out linear interpolation.
neb = NEB(images)
neb.interpolate()
# Run NEB calculation.
qn = FIRE(neb, trajectory='N_diffusion_lin.traj')
qn.run(fmax=0.05)
Step Time Energy fmax
FIRE: 0 11:11:34 9.597339 18.109950
FIRE: 1 11:11:34 6.490830 10.825785
FIRE: 2 11:11:34 5.048270 5.759413
FIRE: 3 11:11:34 4.700705 2.787854
FIRE: 4 11:11:34 4.891328 6.196717
FIRE: 5 11:11:34 4.687828 5.012984
FIRE: 6 11:11:34 4.417121 3.167524
FIRE: 7 11:11:34 4.221284 1.597593
FIRE: 8 11:11:34 4.146848 2.258762
FIRE: 9 11:11:34 4.139218 2.683380
FIRE: 10 11:11:34 4.122955 2.702361
FIRE: 11 11:11:34 4.070613 2.305020
FIRE: 12 11:11:34 3.992069 1.514238
FIRE: 13 11:11:34 3.930763 0.761213
FIRE: 14 11:11:34 3.925234 0.642400
FIRE: 15 11:11:34 3.923535 0.635505
FIRE: 16 11:11:34 3.920250 0.621818
FIRE: 17 11:11:34 3.915601 0.601529
FIRE: 18 11:11:34 3.909894 0.574908
FIRE: 19 11:11:34 3.903492 0.542287
FIRE: 20 11:11:34 3.896780 0.504046
FIRE: 21 11:11:34 3.890121 0.463119
FIRE: 22 11:11:34 3.883188 0.420617
FIRE: 23 11:11:34 3.876387 0.366572
FIRE: 24 11:11:34 3.870123 0.298528
FIRE: 25 11:11:34 3.864694 0.262855
FIRE: 26 11:11:35 3.860431 0.306448
FIRE: 27 11:11:35 3.857149 0.320033
FIRE: 28 11:11:35 3.855593 0.275279
FIRE: 29 11:11:35 3.855418 0.217853
FIRE: 30 11:11:35 3.855185 0.262622
FIRE: 31 11:11:35 3.852924 0.252991
FIRE: 32 11:11:35 3.848397 0.191162
FIRE: 33 11:11:35 3.844221 0.116395
FIRE: 34 11:11:35 3.843042 0.126261
FIRE: 35 11:11:35 3.842802 0.115499
FIRE: 36 11:11:35 3.842384 0.095388
FIRE: 37 11:11:35 3.841892 0.069953
FIRE: 38 11:11:35 3.841432 0.061612
FIRE: 39 11:11:35 3.841070 0.051994
FIRE: 40 11:11:35 3.840809 0.058479
FIRE: 41 11:11:35 3.840598 0.067736
FIRE: 42 11:11:35 3.840367 0.063131
FIRE: 43 11:11:35 3.840120 0.045680
np.True_